Eschergrams

This program is based upon a pseudo routine by Clifford Pickover, which was inspired by the tiled drawings of Escher. In this program the two 8 line routines (if wwu=) draw either a 50x50 pixel tile or the same tile turned upside down. Which tile to draw is decided at random. That is all there is to it. The program has been made a bit more complex by a deliberate attempt to show where the variable values come from. It can be shortened if required by replacing some formulae by values.

' Eschergrams by Clifford Pickover
' from Algorithm 4.2 June 1993
' for sdlBasic (Windows, Unix etc etc)
'  S Shaw, 2013
wd=800
SetDisplay(wd,wd,16,2)
RANDOMIZE
 WHILE INKEY<>k_esc
xof=50 : yof=50 : dx=50 : dy=50 : jum=(wd-dx-dx)/dx
cls
for j=1 to ((wd-dx-dx)/50)*((wd-dx)/50)
  wwu=int(rnd(999999999)/1000000000))
  if wwu=0 then

    line(0.2*dx+xof,0.0*dy+yof,0.0*dx+xof,0.2*dy+yof)
    line(0.4*dx+xof,0.0*dy+yof,0.0*dx+xof,0.8*dy+yof)
    line(0.6*dx+xof,0.0*dy+yof,0.2*dx+xof,1.0*dy+yof)
    line(0.8*dx+xof,0.0*dy+yof,1.0*dx+xof,0.2*dy+yof)
    line(0.0*dx+xof,0.4*dy+yof,1.0*dx+xof,0.8*dy+yof)
    line(0.0*dx+xof,0.6*dy+yof,0.8*dx+xof,1.0*dy+yof)
    line(1.0*dx+xof,0.4*dy+yof,0.4*dx+xof,1.0*dy+yof)
    line(1.0*dx+xof,0.6*dy+yof,0.6*dx+xof,1.0*dy+yof)
  end if
  if wwu=1 then
    line(0.2*dx+xof,0.0*dy+yof,1.0*dx+xof,0.4*dy+yof)
    line(0.4*dx+xof,0.0*dy+yof,0.0*dx+xof,0.4*dy+yof)
    line(0.6*dx+xof,0.0*dy+yof,0.0*dx+xof,0.6*dy+yof)
    line(0.8*dx+xof,0.0*dy+yof,0.4*dx+xof,1.0*dy+yof)
    line(0.0*dx+xof,0.2*dy+yof,1.0*dx+xof,0.6*dy+yof)
    line(0.0*dx+xof,0.8*dy+yof,0.2*dx+xof,1.0*dy+yof)
    line(1.0*dx+xof,0.2*dy+yof,0.6*dx+xof,1.0*dy+yof)
    line(1.0*dx+xof,0.8*dy+yof,0.8*dx+xof,1.0*dy+yof)
  end if
  xof=xof+dx
  if j mod jum=0 then
    yof=yof+dy : xof=50
  end if
  if yof>(wd-dx) then
    yof=50
  end if
  next
waitkey
wend
end

In this example the tile has lines which for the most part cross each other. But if the tile is designed so that no lines cross each other, it could be used in random maze generation. As well as 180 degree rotation, tiles can be rotated by 90 or 270 degrees. A clear path could then be made by manually adjusting the orientation of selected tiles.

Sierpinski Fun

My first sdlbasic page has a listing to produce a Sierpinski triangle and mentioned several ways to obtain one. Here is another one. The rules are really simple. Take a piece of paper. Place a dot anywhere upon it. Then place further dots according to three simple rules. That is all this program does. Because the initial few dots are truly random and may occur outside the final image, we don't draw them. But that image will occur whereever the first dot is drawn.

' triangle fun by charles kluepfel from
' recreational and educational computing 
' (REC) Vol 4 No 4 June 1989
' REC ceased publication January 2007
' for sdlbasic by stephen shaw 2013
dw=1000 : dh=600
setdisplay(dw,dh,16,2)
cls : ct=0
randomize

xtl=0 : ytl=0 : xtr=dw-30 : ytr=0 : xbm=xtr/2 : ybm=dh-20

' first random dot - not drawn

x=rnd(xtr) : y=rnd(ybm)
locate(2,20) : prints("hold esc to exit")
  WHILE inkey<>k_esc
  ct=ct+1
  ' select one two or three:
  rch=int(rnd(999999999)/1000000000*3)+1
  if rch=1 then
    x=x/2 : y=y/2
  end if
  if rch=2 then
    x=(x+xtr)/2 : y=y/2 :
  end if
  if rch=3 then
    x=(x+(xtr/2))/2 : y=(y+ybm)/2
  end if
  if ct>12 then
    dot(x+5,y+10)
  end if
  END WHILE
  end

The magazine REC is beginning (2023) to become available online- developments are developing, so keep an eye on the website Recreational and Educational Computing

Lorenz Attractor

E N Lorenz was working on weather prediction. Simplification of his differential equations left three, represented here by what we do below to change the variables x,y and z. The plot will always end up more or less the same (the attractor) but with some variations as we vary the three variables starting points.

' Lorenz Attractor from algorithm 
'   by Clifford A  Pickover
' from Algorithm 1.2  February 1990
' for sdlBasic (Windows, Unix etc etc)
'  S Shaw, 2013
wd=800
SetDisplay(wd,wd,16,2)
RANDOMIZE
 ' initial values:
 h=0.0025 : x=0.06 : y=0.06 : z=0.06
 WHILE INKEY<>k_esc
 cls

 fracvar=8/3
 for i = 1 to 100000
   xnew=x+10*h*(y-x)
   ynew=y+h*(28*x-y-x*z)
   znew=z+h*(x*y-z*fracvar)
   x=xnew : y=ynew : z=znew
   dot(-x*12-400,y*12+400)
 next
 fprints("hold esc to exit, space for ")
 fprints("different random variable starting points")
waitkey
' what do tiny changes to the initial variables do?
if inkey=32 then
' random variations on the three variables

x=0.03+rnd(999)/10000 : y=x+rnd(999)/10000 : z=x+rnd(999)/10000

   end if
wend
end

Because we are tracking an orbit, this is one routine where the finished result is improved by using line instead of dot. Make the following amendment- notice that x=xnew etc has been slightly relocated:

.....
 znew=z+h*(x*y-z*fracvar)
 line(-x*13-400,y*13+400, -xnew*13-400,ynew*13+400)
 x=xnew : y=ynew : z=znew
 wait(1)
next
....

The wait(1) above slows plotting down and allows you to see the orbits, just remove it to go back to full speed.

Symmetric Attractors

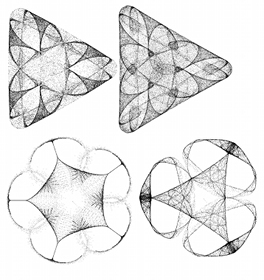
This is based upon an article by Uwe Quasthoff of Leipzig, from Fractal Report issue 21, June 1992. I have included several interesting attractors- I think the last three are my discoveries. I did try using random values but the majority of orbits just disappear off into the distance.

' functions with symmetric attractors 
'  for sdlbasic  (Windows, Unix etc etc)
'  S Shaw, 2013
SetDisplay(800,800,16,2)
RANDOMIZE

a=1 : b=0 : c=0.5 : m=3 : l=-1.804 : scale=80 : xoff=80

x=0.01 : y=0.01 : dta=0

  WHILE INKEY<>k_esc
cls
for olp=1 to 100000
  u=x*x+y*y : xx=1 : yy=0
  for i=1 to m-1
    xxn=xx*x-yy*y
    yy=xx*y+x*yy : xx=xxn
  next
  v=xx*x-yy*y : x=(a*u+b*v+l)*x+c*xx
  y=(a*u+b*v+l)*y-c*yy
  xb=xoff+scale*x : yb=100+scale*y
  dot(4*xb,4*yb)
next
locate(1,1) :   prints ("ESC to exit, n for next  ")
locate(48,58): fprints("a b c  m  l")

locate(48,59): fprints(a) : fprints(" ") : fprints(b) : fprints(" ")
fprints(c) : fprints(" ") : fprints(m) : fprints(" ") : fprints(l)
WAITKEY
IF INKEY=78 OR INKEY=110 THEN
dta=dta+1 : x=0.01 : y=0.01
if dta=1 then
a=2 : b=-0.2 : c=1.0 : m=3 : l=-1.750 : scale=130 : xoff=80
end if
if dta=2 then
a=-1 : b=0.1 : c=-0.8 : m=3 : l=1.520 : scale=70 : xoff=110
end if
if dta=3 then
a=-2 : b=0.0 : c=-0.5 : m=5 : l=2.60 : scale=75 : xoff=105
end if
if dta=4 then
a=-1 : b=0.1 : c=-0.8 : m=5 : l=1.30 : scale=90 : xoff=100
end if
if dta=5 then
a=5 : b=2.0 : c=1.0 : m=6 : l=-2.70 : scale=110 : xoff=100
end if
if dta=6 then
a=5 : b=2.0 : c=1.0 : m=6 : l=-2.585 : scale=110 : xoff=100
end if
if dta=7 then
a=1 : b=0.04 : c=0.1 : m=7 : l=-2.065 : scale=70 : xoff=100
end if
if dta= 8 then
a=-4 : b=1.322 : c=-0.512 : m=3 : l=2.64 : scale=80 : xoff=100
end if
if dta=9 then
a=-4 : b=1.322 : c=-0.512 : m=9 : l=2.65 : scale=80 : xoff=100
end if
if dta=10 then
a=4 : b=0.244 : c=0.599 : m=6 : l=-2.75 : scale=80 : xoff=100
end if
if dta=11 then
a=1.0 : b=0.0 : c=0.5 : m=3.0 : l=-1.804 : scale=80 : xoff=100
dta=0

   end if
end if
wend
END

Henon Chaos

This one is essentially circular. If you start with a value of a, increment it slowly and save the resulting images, they can be animated to produce a strangely wobbly distorting circular pattern.
Fractal Report Issue 4 pdf

' henon attractors using sdlBasic 
'   (Windows, Unix etc etc)
' from "Henon Maps" by Andy Lunness 
'      of Bury, Lancs, from
' Fractal Report Issue 4 (undated)
'             S Shaw, 2013
SetDisplay(800,800,16,2)
' initial values
scale=510  : ofs=350 : n=1
randomize
fprints (" ...a moment...   a=")
a=0+(rnd(999)/10000)*3
  if abs(a)<0.20 then

    a=a+.4
  end if
fprints(a)
WHILE INKEY<>k_esc
   for  x=-0.1 to .8 step .07
      for y=-0.1 to .8 step  .07
         lx=x : ly=y
         for n=1 TO 700
            'gives a reasonable image
              n=n+1
              IF abs(lx+ly)>3010 THEN
                  n=90000
              end if
         xx=lx*cos(a)-(ly-lx*lx)*sin(a)
         ly=lx*sin(a)+(ly-lx*lx)*cos(a)
         lx=xx
         DOT (ly*scale+ofs,lx*scale+ofs)
    next : next : next
 locate(42,3)
 fprints ("ESC to exit or space for another")
 WAITKEY
 if inkey=32 then
   cls
   n=0
   fprints (" ...a moment...   A=")
   a=RND(9999)/10000*3
   if abs(a)<0.2 then
      a=a+.3
   end if
   fprints(a)
   end if
WEND
END

Ikeda Mapping

Not a great deal of variation in this one, but the random plots do differ slightly. Fractal Report 7 pdf

' ikeda attractors using sdlBasic
'    (Windows, Unix etc etc)
' from John Corbit in Fractal Report No 7 (undated)
'          S Shaw, 2013

SetDisplay(800,800,16,2)
' initial values
scale=250  : ofs=300
x=0 : y=0 : p=7.7
' if p<7.2688 the attractor is restricted
randomize
fprints (" ...a moment...   p=")

fprints(p) : fprints("-hold ESC to exit, SPACE for another")

WHILE INKEY<>k_esc
  for n=1 to 250000
    theta=0.4-(p/(1+(x^2+y^2)))
    x1=0.85+0.9*x*cos(theta)-0.9*y*sin(theta)
    y1=0.9*x*sin(theta)+0.9*y*cos(theta)
    dot(y1*scale+ofs*1.4,x1*scale+ofs)
    x=x1 : y=y1
  next
  fprints("    * done * ")
  WAITKEY
  if inkey=32 then
    p=7.2689+rnd(9999)/10000*2+rnd(10000)/10000
    cls
    fprints (" ...a moment...   p=")

fprints(p) : fprints(" -hold space for another, ESC to end")

  end if
WEND
END

Martin's Mapping

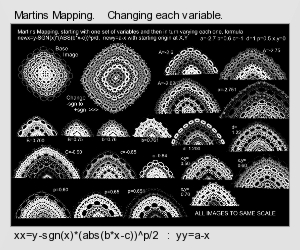
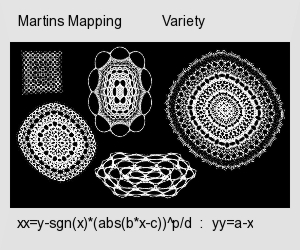
This is one of my favorites and it originated from Dr Barry Martin of Aston University, Birmingham. I understand that it appeared in Scientific American (but I haven't seen that one), and was published in The Armchair Universe (1988) by A K Dewdney. It was repeated in Fractal Report Issues -1 and    0   , and later in issue 9 by Paul Gailiunas, whose slight modification I have indicated below. The main listing follows Barry Martin's original. This little program is capable of so many interesting variations. I have added zoom in and out- adding pan up/down/left/right can be done by modifying the value of variable ofs. There is a family of images from this one. At the end of the listing are links to images from further variations- click the thumbnail for larger image.

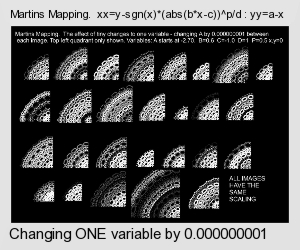
Note that very small variations can have a large affect on the image- I have prepared an image showing variations in just one variable of as small as 0.000000001. This suggests that variations in PC math accuracy may cause an effect.

' martins mappings - attractors using sdlBasic 
'    (Windows, Unix etc etc)
' The variation by Paul Gailiunas is from 
'    Fractal Report No 9 (May 1990)
'       S Shaw, 2013  
SetDisplay(800,800,16,2)
randomize
' initial values
scale=7  : ofs=370
x=0 : y=0 : limit=250000
a=rnd(9999)/5002*2-rnd(9999)/5002*2
b=rnd(200)/100-rnd(200)/100+.0001
c=rnd(300)/100-rnd(300)/100+.0001
fprints ("  a:   b:   c:   ...a moment...")
locate(6,1) : fprints(a) 
fprints("   ") : fprints(b)
fprints("   ") : fprints(c)
fprints("-hold ESC to exit, SPACE for another")
fprints(" i and o to zoom in and out")
WHILE INKEY<>k_esc
  for n=1 to limit
  dot(x*scale+ofs,y*scale+ofs*1.1) 
    ' Barry Martin used 
  xx=y-sgn(x)*(abs(b*x-c)^0.5)
   ' variation by Paul Gailiunas 
   '    is xx=y-sgn(x)*(b*x-c)   
   ' variations well worth exploring 
  '     include using 
  ' other powers (^0.1 to ^0.9)
  ' and or using fractions eg 
  ' xx=y-sgn(x)*(abs(b*x-c)^p/d)
  '   with p<1 and d from 1 to 5)
  yy=a-x
  x=xx : y=yy
  next
  fprints("    * done * ")
  WAITKEY
  if inkey=32 then
      cls : x=0 : y=0
      a=rnd(9999)/5002*2-rnd(9999)/5002*2
      if rnd(100)<25 then
        a=a/2+.2
      end if
      b=rnd(200)/100-rnd(200)/100+.0001
      c=rnd(300)/100-rnd(300)/100+.0001

fprints (" a: b: c: ...a moment... ")
locate(6,1) : fprints(a) : fprints(" ")
fprints(b) : fprints(" ") : fprints(c) : locate(3,3)
fprints("-hold ESC to exit, SPACE for another, i to zoom in, o to zoom out")

  end if
  IF INKEY=73 OR INKEY=105 THEN
    scale=scale*1.4
    cls : x=0 : y=0
  END IF
  IF INKEY=79 OR INKEY=111 THEN
    scale=scale*0.7
    cls : x=0 : y=0
  END IF
WEND
END

Pickover Butterfly

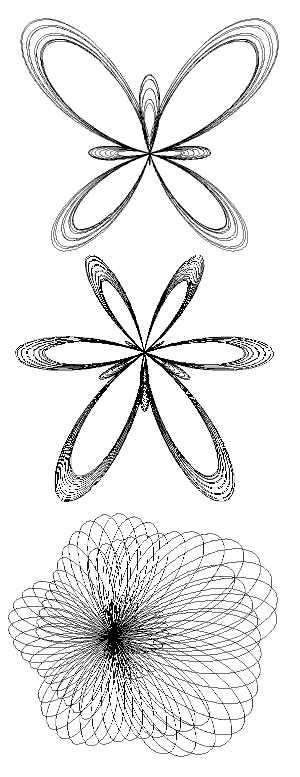
Taken from Clifford A Pickover's book "Computers and the Imagination" published in 1991. Clifford references an earlier article "The Butterfly Curve" by Temple Fay in "American Math Monthly 96(5)".

' random butterflies  using sdlBasic 
'    (Windows, Unix etc etc)
'  S Shaw, 1990-2013 from Computers and the 
'     Imagination, Pickover, 1991
SetDisplay(800,800,16,2)
scale=80 : ofs=400 : flag=0
WHILE inkey<>k_esc
  if flag=0 then
    pi=3.1415 :  cv1=2 : cm1=4 :sp1=5 : sd1=12
  end if
  if flag=1 then
    cv1=2.1 : sp1=7 : sd1=30 : cm1=6
  end if
  for theta=0 to 100*pi step 0.010
     r=exp(cos(theta)) - cv1*cos(cm1*theta)+(sin(theta/sd1))^sp1
     x=r*cos(theta) : y=r*sin(theta)

     yy=(x*scale)+ofs : xx=(y*scale)+ofs
     if theta=0 then
        oldx=xx : oldy=yy
     end if
     if theta<>0 then
       line(oldx,oldy,xx,yy)
       oldx=xx : oldy=yy
     end if
  end for
  locate(1,1) 
  prints ("ESC to exit, space for alternative image ")
  WAITKEY
  if inkey=32 then
    cls
    wait(65)
    flag=(flag=0)
' above line switches flag between 0 and 1
  end if
WEND
END

Butterfly Variations

I love to try different values in these programs so here is a program that throws a bit of randomness into the butterfly program.
In the program above and below, in the line for t=1 to n step p, the value of the step p will control how smooth the curves are- go for a small value of p if you have a large hi res display and want to see smoother plots. The value of n decides how complex the figure is- for a stable butterfly you can go to high values and get a good image, but for more unstable images quite a low value is often better- perhaps as low as 30 in some cases. With low values of n you are more likely to see the line just stop.

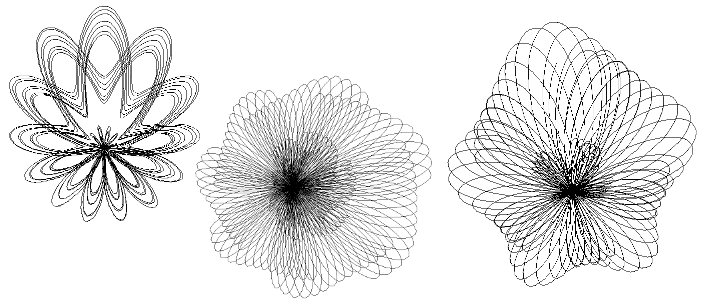
' random complex butterflies  using sdlBasic 
'     (Windows, Unix etc etc)
'  S Shaw, 1990-2017 from Computers and the
'       Imagination, Pickover, 1991
' butterfly 2- added randomness for weirder shapes
randomize
SetDisplay(800,800,16,2)
flag=0
 WHILE inkey<>k_esc
a=(rnd(999)/1000)*3+1
b=(rnd(999)/1000)*4+3
c=(rnd(999)/1000)*5+3
d=10+40*rnd(999)/1000

test=rnd(999)/1000
if test<0.2 then
c=int(c)
end if

a=int(a*10)/10:b=int(b*10)/10:c=int(c*10)/10:d=int(d*10)/10

if c<>int(c) then
flag=1
end if

for t=0 to 62.8 step (3.1415/110)
' full image to 314.15 instead -
' as listed the image is simpler- but incomplete
' make step size smaller for smoother image.

  if flag=0 then
  q=sin(t/d)^c
  else
  q=abs(sin(t/d))^c
  end if

  r=exp(cos(t))-a*cos(b*t)+q
  x=r*cos(t):y=r*sin(t)
  xx=x*58+360
  yy=y*58+360

  if t=0 then
  oldx=xx:oldy=yy
  end if

  line(oldx,oldy,xx,yy)
  oldx=xx:oldy=yy

end for

locate(1,1) : prints ("ESC to exit, space for alternative image ")

  WAITKEY
if inkey=32 then
cls
wait(65)
flag=(flag=0)
end if
WEND
END 

Dot Moire Spiral

Random Dot Moire Patterns
This category of image was brought to light by Leon Glass in 1969, whilst studying visual perception. We take a random set of dots, then slightly enlarge the image, place it over the first, and rotate slightly. With a small rotation we see a spiral, but there really isn't one. With a larger rotation the perception is lost. The coding is based upon page 45 of Clifford A Pickover's 1990 book "Computers Patterns Chaos and Beauty".

See what effect minor manipulations have. There are possibilities for some interesting animations here!

'  image  using sdlBasic 
'   (Windows, Unix etc etc)
'  s shaw for ti99/4a 1990 for sdlbasic 2014
' from COMPUTERS PATTERN CHAOS 
'    AND BEAUTY by Clifford A Pickover
' MOIRE DOT PATTERN
' an=rotation in degrees; sz=size in pixels
SetDisplay(800,800,16,2)
pi=3.1415926
RANDOMIZE
' initial rotate and enlarge
AN=1.7 : AN=AN*PI/180 : ENL=1.11
 SZ=600 : MD=SZ/2 : j=1

WHILE INKEY<>k_esc
cls
RANDOMIZE
j=1

FOR I=1 TO 13000
 RANDX=RND(SZ) : RANDY=RND(SZ)
dot(RANDX,RANDY)

RANDXX=ENL*((RANDX-MD)*COS(AN)+(RANDY-MD)*SIN(AN))+MD
RANDY=ENL*((RANDY-MD)*COS(AN)-(RANDX-MD)*SIN(AN))+MD

 RANDX=RANDXX
dot(RANDX,RANDY)
 NEXT

prints("ESC to end, c=increase rotation a=decrease rotation")
fprints("t=random rotate only, e=random rotate and enlarge")

 WAITKEY

' increase rotation =c
IF INKEY=67 OR INKEY=99 THEN
AN=AN*1.1
 CLS
END IF

'decrease rotation =a
IF INKEY=65 OR INKEY=97 THEN
 CLS
 AN=AN*0.94
END IF

' rotate only - reset - random =t
IF INKEY=84 OR INKEY=116 THEN
 CLS
 AN=1.7 : AN=AN*PI/180
 ENL=1.00
END IF

' rotate and enlarge- reset - random =e
IF INKEY=69 OR INKEY=101 THEN
 CLS
 AN=1.25 : AN=AN*PI/180
 ENL=1.04
 END IF

 FOR I=1 TO 400000
 j=cos(i)
 NEXT
 'AVOID FLICKER

WEND
END

banthorpe plot

I came across this one a long long time ago- my notes originate from 1982. Alas I cannot recall the origin of the plot but the full name of the creator is Malcolm Banthorpe who used an Acorn computer and was a VT editor for the BBC also did visual work for the BBC (Blakes 7 etc). I like the way this 3d image is plotted.

' banthorpe 3d graphic  for sdlbasic  
'   (Windows, Unix etc etc)
'  S Shaw, 2015
SetDisplay(800,600,16,2)
cls

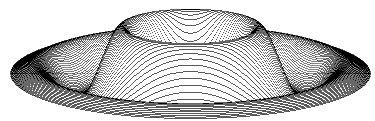
M1=720
V=620
X1=M1/2
X2=X1^2
Y1=V/2
Y2=V/4

    FOR X5=0 TO X1

     X4=X5^2
     M=-Y1
     A=SQR(X2-X4)

       FOR I1=-A TO A STEP 5
      ' the step figure defines the density
       R1=SQR(X4+I1^2)/X1
       F=(R1-1)*SIN(R1*12)
      ' the above line is the function plotted
       R=INT(I1/4+F*Y2)
      ' the divisor 4 in the line above
      ' is the degree of tilt of the figure

         IF R>M  THEN
         M=R
         R=Y1-R
         C=X1-X5+60
         DOT(C,R)
         C=X1+X5+60
         DOT(C,R)
         END IF
       NEXT
    NEXT
WAITKEY
END

Twisted

' based upon: X(T+1)=R*X(T)*(1-X(T))
' Source: L D Magguilli writing in
' ALGORITHM Oct-Dec 1992, Volume 3 Number 4.

' He cites M Szyszkowicz.
' by s shaw for ti99/4a November 1992 TI*MES No 39
' by s shaw for sdlbasic December 2015

SetDisplay(800,800,16,2)
fprints (" ...a moment...")
sw=750 : sh= 750 : rs=3.5 :: re=4
dr= (re-rs) /sh : xs=0 : xe=0.5
' vary the value of sc
dx=( xe-xs) /sw : it=3 : sc=29
WHILE INKEY<>k_esc
for j = 1 to sh
r=re-j*dr

for i=1 to sw
x=xs+i*dx
y=x

for k=0 to it
x=r*x*(1-x)
NEXT

k=int(sc*abs(x-y))

if k/2<>int(k/2) then
dot(j,i)
end if

next
next

fprints(" * done * ")
WAITKEY
WEND
END

' suggested modifications:
' after x=r*x*(1-x) add another line
' x=3*x*(1-x)

' or replace k=int(sc*abs(x-y)) with
' k=int(sc*x)

' or add colour eg with:
' k=int(sc*abs(x-y))
' pc=k mod 64000
' pc=pc*8000000+2000000
' if k/2<>int(k/2) then
' plot(j,i,pc)
' end if